ch11 死锁

死锁问题

死锁 deadlock；是一组阻塞的进程，每个进程都持有一个资源并等待获取另一个进程持有的资源。

死锁的示例：交通桥

如图所示，桥是资源，进程是车辆，两个不同方向的车辆同时占用桥，此时发生谁也过不去的情况（死锁的发生）；

• 当死锁发生时，如果一辆车倒车（抢占资源和回滚）就可以解决死锁问题
• 死锁发生时，可能需要后退多台车辆
• 饥饿，而饥饿并不一定是死锁

系统模型

在正常情况下，进程必须在使用之前请求资源，并在完成后释放它，顺序如下：

• 请求：如果不能立即授予请求，则进程等待，直到它需要的资源变得可用。例如，系统调用 open()、malloc()、new() 、request() 等。

• 使用：进程使用资源，例如文件中读取数据；使用硬件。

• 释放：进程完成后放弃资源，以便其可用于其他进程。如，close()、free()、delete() 、 release()。

当在集合中的每个进程都在等待当前分配给集合中另一个进程的资源时，这一组进程就会发生死锁

资源分配

通过实例来理解死锁，

• 一组资源：

  • ${ R_1,\ R_2,\ R_3,\ ….,\ R_N }$；为方形，图形内的点代表资源数量

• 一组进程：

  • ${ P_1,\ P_2,\ P_3,\ ….,\ P_N }$

• 请求边缘 Request Edge：进程需要一些资源，被称为请求边缘；如 $P_i\ →\ R_j$

• 分配边缘 Assign Edge：当资源已经被分配给进程，被称为分配边缘；如 $R_j\ →\ P_i$

• 当请求被授予时，可以通过反转方向的线将请求边缘转换为分配边缘

类型	示意图
Process
Resource
$P_i$ 请求的 $R_j$ 实例
$P_i$ 持有一个 $R_j$ 的实例 也可以说 $R_j$ 被 $P_i$ 所持有

资源分配图

资源分配图

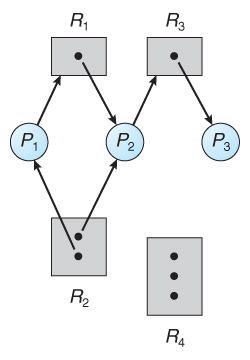
如图所示，资源类型为：

• P = ${P_1,\ P_2,\ P_3}$
• R = ${R_1,\ R_2,\ R_3,\ R_4}$
• RE = ${P_1\ →\ R_1,\ P_2\ →\ R_3}$
• AE = ${R_1\ →\ P_2,\ R_2\ →\ P_2,\ R_2\ →\ P_1,\ R_3\ →\ P_3}$
  • ${P_1}$ 持有 ${R_2}$ 等待 ${R_1}$
  • ${P_2}$ 持有 ${R_1}$ 和 ${R_2}$ 等待 ${R_3}$
  • ${P_3}$ 持有 ${R_3}$

死锁示意图

资源分配图不包含循环，则不会死锁；如果有向图为环形，则为死锁，例如

环形有向图

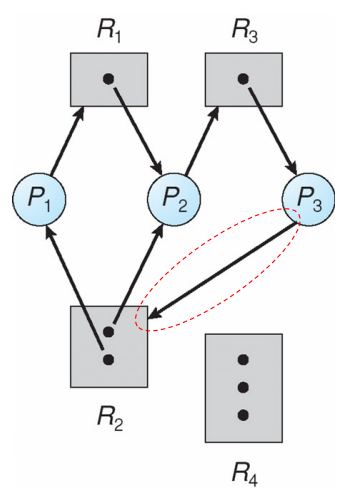
死锁示意图资源类型为：

• P = ${P_1,\ P_2,\ P_3}$
• R = ${R_1,\ R_2,\ R_3,\ R_4}$
• RE = ${P_1\ →\ R_1,\ P_2\ →\ R_3,\ P_3\ →\ R_2 }$
• AE = ${R_1\ →\ P_2,\ R_2\ →\ P_2,\ R_2\ →\ P_1,\ R_3\ →\ P_3}$
  • ${P_1}$ 持有 ${R_2}$ 等待 ${R_1}$
  • ${P_2}$ 持有 ${R_1}$ 和 ${R_2}$ 等待 ${R_3}$
  • ${P_3}$ 持有 ${R_3}$ 等待 $R_2$

这个图出现两个环形，这种情况下会发生死锁

• $P_1\ →\ R_1\ →\ P_2\ →\ R_3\ →\ P_3\ →\ R_2\ →\ P_1$
• $P_2\ →\ R_3\ →\ P_3\ →\ R_2\ →\ P_2$

有环但无死锁

有环但无死锁

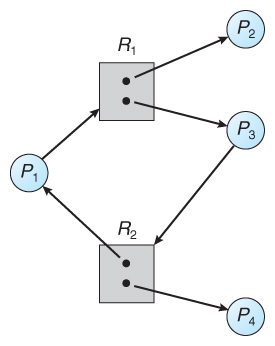
有环但无死锁意图资源类型为：

• P = ${P_1,\ P_2,\ P_3,\ P_4}$
• R = ${R_1,\ R_2}$
• RE = ${P_1\ →\ R_1,\ P_3\ →\ R_2 }$
• AE = ${R_1\ →\ P_2,\ R_1\ →\ P_3,\ R_2\ →\ P_4,\ R_2\ →\ P_1}$
  • ${P_1}$ 持有 ${R_2}$ 等待 ${R_1}$
  • ${P_2}$ 持有 ${R_1}$
  • ${P_3}$ 持有 ${R_1}$ 等待 $R_2$
  • ${P_4}$ 持有 ${R_2}$

此图中，$P_4$ 执行完会释放 $R_2$，$R_2$会被分配给 $P_3$，这样就跳出了循环

结论

• 如果图中没有循环，则无死锁
• 如果图中，一个资源仅包含一个实例，必然会发生死锁
• 如果图中，一个资源包含多个实例，则可能会发生死锁

死锁特性

必要条件

• 实现死锁需要四个条件：
  • Mutual Exclusion：至少一个资源必须以不可共享的方式持有；如果任何其他进程请求此资源，则该进程必须等待资源被释放。
  • Hold and Wait：一个进程必须同时持有至少一个资源并等待至少一个当前被其他进程持有的资源。
  • No preemption：一旦进程持有资源，则该资源不能从该进程中被抢占，直到该进程自愿释放。
  • Circular Wait ：一组等待的进程 ${P_0,\ P_1,\ P_2,\ …,\ P_N}$ 必须存在每个 $P[ i ] $ 都在等待 $P[ ( i + 1 ) % ( N + 1 )]$

死锁处理方法

• 确保系统永远不会进入死锁
• 允许系统进入死锁状态，然后恢复
• 忽略这个问题，假装系统中从来没有发生死锁，用于大多数操作系统,包括UNIX

死锁预防

限制资源的申请方式

• 互斥

  • 对于只读文件资源来说不会引起死锁
  • 对于只允许单独访问的资源，需要互斥，如打印机

• 等待：必须确保进程在访问资源时，没有持有其他资源

  • 要求对所有进程同时请求所有资源。这种情况下当一个资源被占用，导致等待很长时间，这可能会浪费系统资源。
  • 只有当进程能够获得旧的资源以及它请求新的资源，进程才可以执行
  • 这种情况资源利用率低，饥饿

• 非抢占式：以下情况下可以防止死锁

  • 如果进程占有某些资源，并请求其他不能被立即分配的资源，则释放当前正占有的资源（可能资源浪费）
  • 当请求资源不可用时，并本身属于阻塞；这时资源会被抢占，添加到进程等待资源列表中

• 循环等待

  • 对所有资源进行编号排序，并要求进程仅以严格的递增（递减）顺序请求资源（常见于嵌入式操作系统）
  • 如：为了请求资源 $R_j$，进程必须首先释放所有的 $R_i$，使得 $i >= j$
  • 挑战性：如何确定不同资源的排序

避免死锁

死锁避免，与死锁预防的区别是，死锁预防是确保可以预防死锁必要条件的其中一个；死锁避免是确保进程不会导致死锁。

要想防止死锁，就需要更多有关进程的信息，这样的话会导致系统资源利用率低（保守方法），根据不同的调度算法，会得到进程所需的资源的数量，还可以知道以什么顺序进行调度。

调取器会根据资源分配状态检测将来是否出现死锁

安全状态

如果系统可以分配所有进程的所有资源，而不进入死锁状态，则被称为安全状态。更严格来讲，存在安全的进程序列，则状态是安全的，（${P_0,\ P_1,\ P_2,\ …,\ P_N }$）

• 如果 $P_i$ 资源的需求不是立即可用，那么 $P_i$ 可以等到所有 $P_j$ 完成

• 当 $i>j$ 时，$P_i$ 要求的资源能够由 $当前可用的资源+所有的\ P_j\ 持有的资源$ 来满足；如果 $P_i$ 完成了并释放了所有资源，那么 $P_j$ 也能够完成

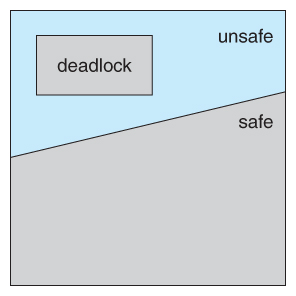
如图所示：如果不存在安全序列，则系统处于不安全状态，这可能会导致死锁。（所有安全状态都是无死锁的，但并非所有不安全状态都会导致死锁。）

例如：考虑一个具有 12 个磁带驱动器的系统，分配如下。这是一个安全的状态吗？安全顺序是什么？

Process	Maximum Needs	Current Allocation
$P_0$	10	5
$P_1$	4	2
$P_2$	9	2

是安全的

• 当 $t=0$ 时，$P_0$ 持有5个资源； $P_1$ 持有 2；$P_2$ 持有 2，此时是安全的；

安全顺序为：

• $P_1$ 可以分配所有的资源；$P_1\ need = Total - Allocation = 12-9=3$，$P_1$ 需要4 ，已分配2，剩余3，可以分配给 $P_1$；当 $P_1$ 执行完成并释放，此时 $available=2+2+1 = 5$
• $P_0$，可用5，已分配5，需要5；此时 $P_2$ 也可以执行；释放 $available=5+5=10$
• $P_2$，可用10，已分配2，需要9；此时 $P_2$ 也可以执行；释放 $available=2+9+1=12$

如果进程 P2 请求并被多分配一个磁带资源，会发生什么情况？

• 会从安全状态变为不安全状态，$P_2$ 当前分配为3 ，此时 $P_1$ 还是可以执行，执行释放完之后，可用为4，不满足 $P_0$ 所需5 ，$P_2$ 所需的6，死锁

资源分配图

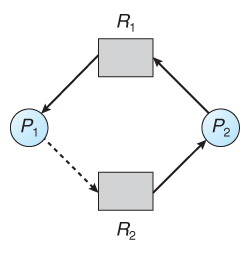
当资源类别仅具有其资源单实例，可以通过资源分配图中循环来检测死锁。这种情况下，使用声明边缘 （claim edge 根据上下文翻译的，不知道对不对），指向了在未来所需要请求的资源，用虚线表示，来避免不安全状态

• 声明边缘 claim edge：未来需要请求的资源
• 请求边缘 request edge：请求的资源
• 进程在请求资源会从 claim edge 转为 request edge
• 进程释放资源会从 assignment edge 转为 claim edge

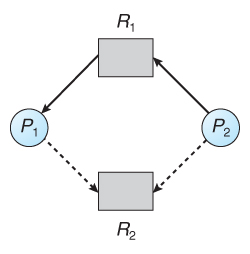
此方法的工作原理是，拒绝会在资源分配图中产生循环的请求，从而使声明边缘生效

图：当生成的资源分配中会形成一个循环，此资源申请无法授予

Reference

Deadlocks

ch7 deadlock

银行家算法

银行家算法 The Banker’s algorithm，是一种资源分配和避免死锁的算法，是通过模拟所有资源的一种”预测“最大可能需求来为进程分配资源是否 安全；这个成为 safe state check

为何被命名为银行家算法？

银行家算法与银行使用相同的手法来检查资金是否可以批给贷款客户，假设一家银行有 N 个账户持有人，他们存入银行的总金额为 M。在分配任何贷款金额之前，银行会检查在从银行的总金额中减去贷款金额后，剩余的钱是否大于 M，大于 M 则分配这笔贷款是安全的，否则不是。

而银行家算法是，在一个进程启动时，必须事先声明它可能请求的最大资源分配数，最高可达系统上可用的数量；在发出请求后，调度器确定分配给该进程资源是否会使系统处于不安全状态。如果是，则该进程等待，直到分配后系统处于安全状态。

银行家算法的数据结构

• n ：进程数

• m：资源数

• $Available[ m ]$：当前每种类型有多少资源可用。

• $Max[n][m]$：每个资源的每个进程的最大需求。

• $Allocation[n][m]$：分配给每个进程的每个资源类别的数量。

• $Need[n][m]$：每个进程每个类型所需的剩余资源。

• $Need[ i ][ j ] = Max[ i ][ j ] - Allocation[ i ][ j ]$

银行家算法需要实现知道每个进程所需的最大资源个数

银行家算法应用

首先需要一个算法来确定特定状态是否安全；算法会根据以下步骤确定系统的当前状态是否安全：

• ⑴ Work 和 Finish 分别是长度为 m 和 n 的向量。
  • Work 是 available 的副本，将在分析期间进行修改。
  • finish 是一个布尔值的向量，表示进程是否完成
  • 初始化时，所有 $Work=Available$ ；$Finish = false$
• ⑵ 运行时，找到满足 $Finish[i] == false$；$Need[i]<Work[i]$；此时可以分配，如果不存在转4
• ⑶ 完成时，设置 $Work = Work + Allocation[i]$，代表释放资源回到 2
• ⑷ 如果所有的 $finish[ i ] == true$，则状态是安全的，因为已经完成并有安全序列

有了具体的规范，就需要看银行家算法本身如何执行，算法确定新请求是否安全，当发出请求时，对其做满足推定（假装被授予），查看结果是否安全，安全则批准，不安全则拒绝，如：

• $Request[ n ][ m ]$，代表当前请求需要的资源数，如果 $Request[ i ] > Need[ i ]$ 则拒绝
• 如果 $Request[ i ] > Available[i]$，那么则需要等待可用。
• 方法是满足推论，会检查结构是否安全，如果是，授予；如果否，则进程等待，直到请求可以被安全授予

整个过程的计算方式是：

• $Available = Available - Request$
• $Allocation = Allocation + Request$
• $Need = Need - Request$

Processes	Allocation A B C	Max A B C	Available A B C
$P_0$	1 1 2	4 3 3	2 1 0
$P_1$	2 1 2	3 2 2
$P_2$	4 0 1	9 0 2
$P_3$	0 2 0	7 5 3
$P_4$	1 1 2	1 1 2

计算每个进程Need，列出矩阵图

$Need = Max – Allocation$

Processes	Allocation A B C	Max A B C	Available A B C	Need A B C
$P_0$	1 1 2	4 3 3	2 1 0	3 2 1
$P_1$	2 1 2	3 2 2		1 1 0
$P_2$	4 0 1	9 0 2		5 0 1
$P_3$	0 2 0	7 5 3		7 3 3
$P_4$	1 1 2	1 1 2		0 0 0

这个是否安全？

• $P_0$ 需要 $(3\ 2\ 1)$，Available为 $(2\ 1\ 0)$；则 $Need <=Available = False$

• $P_1$ 需要 $(1\ 1\ 0)$，Available为 $(2\ 1\ 0)$；则 ==$Need <= Available = True$==

  • $P_1$ 可以授予，执行结束后，$Available = Available +Allocation$
  • $(2, 1, 0) + (2, 1, 2)$ = $(4, 2, 2)$

• $P_2$ 需要 $(5\ 0\ 1)$，Available为 $(4\ 2\ 2)$；则 $Need <=Available = False$.

• $P_3$ 需要 $(7\ 3\ 3)$，Available为 $(4\ 2\ 2)$；则 $Need <=Available = False$

• $P_4$ 需要 $(0\ 0\ 0)$，Available为 $(4\ 2\ 2)$；则 ==$Need <= Available = True$==

  • $P_1$ 可以授予，执行结束后，$Available = Available +Allocation$
  • $(4, 2, 2) + (1, 1, 2)$ = $ (5, 3, 4)$

• $P_2$ 需要 $(5\ 0\ 1)$，Available为 $(5\ 3\ 4)$；则 ==$Need <= Available = True$==.

  • $Available = Available +Allocation$
  • $ (5, 3, 4) + (4, 0, 1)$ = $ (9, 3, 5) $

• $P_3$ 需要 $(7\ 3\ 3)$，Available为 $(9\ 3\ 5)$；则 ==$Need <=Available = True$==

  • $Available = Available +Allocation$
  • $(9, 3, 5) + (0, 2, 0) = (9, 5, 5)$

• $P_0$ 需要 $(3\ 2\ 1)$，Available为 $(9\ 5\ 5)$；则 ==$Need <=Available = True$==

故序列是安全的，安全序列为 $P_1, P_4, P_2, P_3, P_0$

https://angom.myweb.cs.uwindsor.ca/teaching/cs330/ch7.pdf

死锁检测

死锁检测是指如果在不能避免死锁的情况下，检测死锁何时发生，并以某些方式恢复。

对死锁检测会对性能造成影响，除此以外，还必须有策略（算法）来从死锁中恢复，当进程必须被终止或抢占时，那进程工作会丢失

每个资源类型单一实例

(a) 资源分配图     (b) 进程等待图

如图所示：等待图是资料类型的图的变种

• 等待图中从 $P_i\ →\ P_j$ 的线表示进程 $P_i$ 正在等待进程 $P_j$ 持有的资源。
• 等待图中的循环表示死锁
• 算法必须可以做到维护一个等待图，并定期检测死锁循环

死锁检测算法

死锁检测算法与银行家算法基本相同，但有两个差别：

• 银行家算法步骤一中，初始将所有 $Finish[i] = false$。而改算法仅 $Allocation[ i ] \ne 0$，才将 $Finish[ i ] = false$。如果进程分配资源为0，则 $Finish[i] = true$。
  • 假设如果所有其他进程都可以完成，那么这个进程也可以完成。此外，算法会寻找哪些进程涉及死锁情况，没有分配任何资源的进程不能参与死锁。
• 步骤2, 3 与银行家算法一致
• 银行家算法中，如果 $Finish[ i ] == true$ 则不存在死锁。该算法中，如果存在 $Finish[ i ] == false$ ，则检测到死锁。

如：有5个进程 $P_0$ ~ $P_4$；三种资源 $A=7$，$B=2$，$C=6$

Processes	Allocation A B C	Request A B C	Available A B C
$P_0$	0 1 0	0 0 0	0 0 0
$P_1$	2 0 0	2 0 2
$P_2$	3 0 3	0 0 0
$P_3$	2 1 1	1 0 0
$P_4$	0 0 2	0 0 2

这个是否安全？

• $P_0$ request $(0\ 0\ 0)$，执行释放后

  • $Available = Available +Allocation$

  • $(0, 0, 0) + (0, 1, 0)$ = $(0, 1, 0)$

• $P_2$ 同 $P_0$

  • $(0, 1, 0) + (0, 1, 0)$ = $(3, 1, 3)$

• $P_1$ request $(2\ 0\ 0)$，执行释放后

  • $(3, 1, 3) + (2, 0, 0)$ = $(5, 1, 3)$

• $P_3$ request $(2\ 1\ 1)$，执行释放后

  • $(5, 1, 3) + (2, 1, 1)$ = $(7, 2, 4)$

• $P_4$ request $(0\ 0\ 2)$，执行释放后

  • $(7, 2, 4) + (0, 0, 2)$ = $(7, 2, 6)$

估是安全的

检测算法使用

何时，使用什么样的频率来检测依赖于:

• 死锁多久可能会发生？
• 多少进程需要被回滚？ one for each disjoint cycle

这取决于预期死锁发生的频率，已经发生死锁后的后果，（如果发生死锁没有立即恢复，会越来越多的进程导致死锁后得不到资源阻塞）；通常情况下，常用方法：

• 授予的资源分配后进行死锁检测，这样做可以立即检测到死锁；缺点是由于频繁检查死锁而导致性能下降。
• 仅在可能发生死锁的边缘（进程对资源的请求的边）时才进行死锁检测，这样检查频率就会很低，缺点是无法检测到原来死锁所涉及的进程，会导致死锁复杂化，恢复过程复杂
• 保留资源分配的历史日志定期检查死锁（如计时器、CPU资源利用率低）；通过追踪日志确定何时发生死锁以及哪些进程导致了最初的死锁

死锁恢复

通常从死锁中恢复有三种方法：

• 人工干预；终止所有的死锁进程
• 终止一个或多个死锁进程，直到死锁消除
• 抢占资源

进程终止

基本可以恢复死锁的方法：

• 终止所有涉及死锁的进程
• 一个一个的终止进程，直到死锁被消除
  • 这种情况下，很多因素都决定接下来要终止进程的顺序：
  • 优先级
  • 进程运行了多久，还需多久才可完成
  • 进程持有多少资源和什么类型的资源。
  • 进程完成还需多少资源
  • 需要终止多少个进程
  • 进程是交互式的还是批处理
  • 进程是否对任何资源进行了不可逆的更改

资源抢占

• 选择受害者：选择一个进程进行资源抢占，最小成本
• 回滚：返回到一些安全状态,重启进程到安全状态
• 饥饿：同一进程可能一直被选作受害者，包括回滚的数量
  • 使用优先级系统，并在每次进程资源被抢占时增加进程的优先级。最终，获得足够高的优先级，使其不再被抢占。